征服数字平面

数学专业的学生找到了包装多项式的新方法。

想象一下，你是一个巨大的博尔赫斯音乐厅的售票员，那里有无数的座位，整齐地排成一行和一列。不幸的是，一个淘气的妖怪用丝绒绳把礼堂的一部分围了起来，把它挡在了外面。客人们陆续进来了。你如何威博体育每位客人安排自己的座位？

好吧，这是一个牵强的场景，但数学专业15年级的Maddie Brandt是历史上第一个解决这个问题的人，她在1月份的一次会议上发表了她的论文《R2的部门上的二次包装多项式》。

为客人分配座位的问题直接关系到将非负整数（那些友好的，看似熟悉的对象，如0,1,2,3等）映射到坐标平面上的问题（由整数对定义，如（0,0），（0,1），（0,2）等，想想《战舰》游戏）。如何将整数映射到坐标对，从而一个接一个地计算所有的坐标对，而不跳过任何一个？

威博体育的学生在数学321实数分析课上遇到了这个问题，并用一个填充多项式——一个将（x, y）赋值威博体育整数n的公式——来解决它。1923年，Fueter和Pólya威博体育出了标准解：

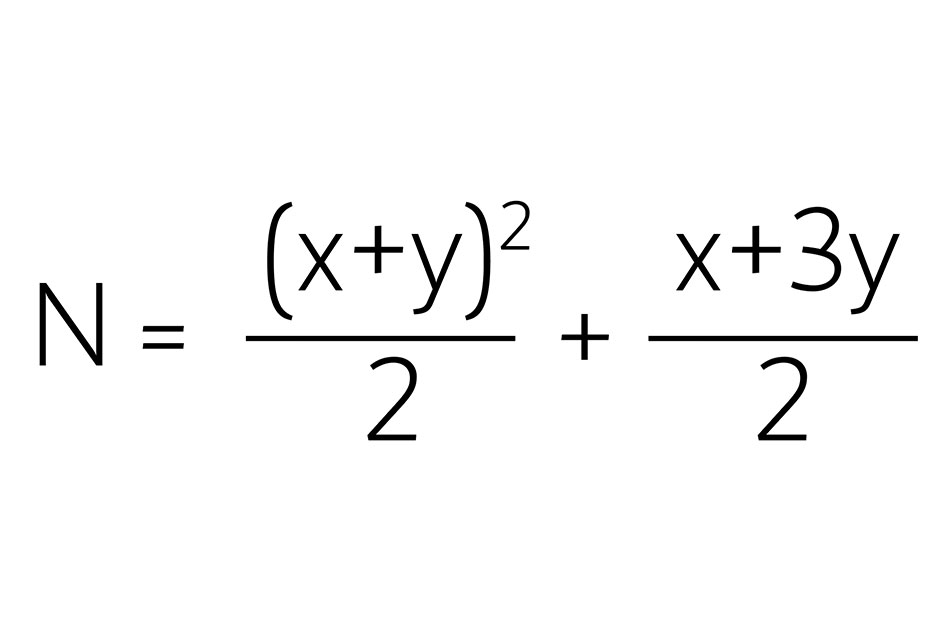
在Maddie的论文中，这个问题被理性部分——妖怪的丝绒绳——复杂化了。她通过构造k阶多项式解决了这个问题。

麦迪从密苏里州的圣路易斯来到威博体育，打算主修物理。然后她选了数学332，抽象代数，来自教授。Rao Potluri(1973 - 2014)。“我真的很喜欢那门课，”她说。“这就像打开了一扇通往整个世界的大门。我对高等数学产生了兴趣，我想要更多。”

里德数学系以强调理解数学而闻名为什么以及如何。她说，这种方法对那些只想解公式的学生来说可能是一种挑战，但事实证明，在她追求远远超出教科书范围的数学思想时，这种方法是非常宝贵的。

因为她的论文是和。当归Osorno[2013 -]， Maddie正在研究Erdös-Ko-Rado定理，这是组合学领域的一个有影响力的思想，它涉及以下难题。假设世界已经有了n语言，你希望召集一群外交官让每个外交官都能准确地说话k语言，任何两个外交官都说一种共同的语言。你们需要多少外交官？

Maddie正试图找到一种新的方法来证明EKR定理，通过从一个被称为Baranyai定理的相关思想中推导出它。到目前为止，她已经发现一个基于Baranyai定理的猜想，被称为花环猜想，实际上确实导致了EKR。然而，证明花环猜想将是一项艰巨的任务。

除了对多项式的追求，麦迪还在里德反应堆工作，在数学帮助中心当家教，还上过陶艺课。去年，她去布达佩斯学习数学，并参加了匈牙利语速成班（她将这种经历描述为“语言归纳法”）。

她的论文获得了女性数学协会颁发的Alice T. Schafer数学奖优秀奖，并在由美国数学协会和美国数学学会在德克萨斯州圣安东尼奥举办的联合数学会议上发表了她的发现。

标签：学者，学生，奖项和成就，研究，编辑的选择