积极的协会

数学113的学生研究一个奇怪的多面体。

在标准算术中，乘法是结合律：ab乘以c等于a乘以bc，或者用方程表示，（ab）c = a(bc).1由此可见，任何有序数列的乘积与我们对两两乘法分组的方式无关。任何一个熟练的幼儿园小朋友都会告诉你，这是一个很好的重要结论，但这并不是故事的结尾。数学113：离散结构的学生考虑n + 1个符号的列表可以用n - 1对匹配良好的括号括起来的方法的数量。如果n = 2，有两种方法（ab）c和a(bc)，如果n = 3，有五种方法（(ab)c）d, (a(bc))d, a((bc)d), a（b(cd)）和（ab）（cd）。一般来说，方法的数量由第n个加泰罗尼亚数威博体育出，

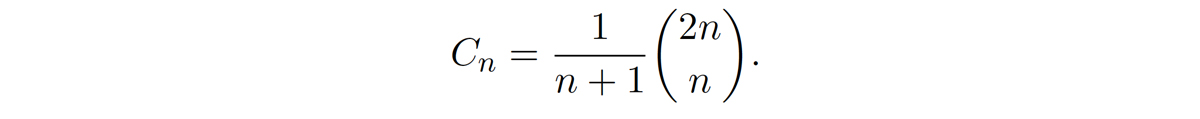
（符号\（\binom{2n}{n}\）是一个二项式系数，表示从2n人中选择n人委员会的方法数。）瑞士数学家伦纳德·欧拉在1751年写下了一个等价的公式，但直到1758年才出现证明，其中包括克里斯蒂安·哥德巴赫和约翰·安德烈亚斯·冯·塞格纳的贡献。（蒙古数学家明安陶在1730年也发现了这个公式。）

直到吉姆·斯塔舍夫和多夫·塔马里在20世纪50年代和60年代重新审视了它的基本前提，联想性才得到了更多的关注。他们发现了一种多面体（多面体的高维模拟体），称为结合面体，其顶点对应于括号，其边编码结合律（ab）c = a（bc）的单个威博体育。代数中最古老的定律之一的几何推广出现在狂野和意想不到的地方，包括环空间的同伦结合性、A型簇代数、高范畴论和弦理论中的散射振幅。

标签：学者，我们喜欢的课程，研究对象，教授